Tấn công Lattice trong Cryptography là gì?

Tấn công Lattice (Lattice Attacks) trong Cryptography là một phương pháp tấn công được sử dụng trong mật mã học để tìm ra khóa bí mật từ khóa công khai. Nó dựa trên lý thuyết mạng lưới và giải thuật thu nhỏ cơ sở mạng lưới.

Click Digital sẽ giải thích rõ hơn về tấn công Lattice trong bài viết này.

Mạng lưới (Lattice) trong Cryptography là gì?

Chúng ta cùng tìm hiểu về Mạng lưới (Lattice) và Giải thuật thu nhỏ cơ sở mạng lưới (Lattice Basis Reduction) nhé.

1. Mạng lưới (lattice) là gì?

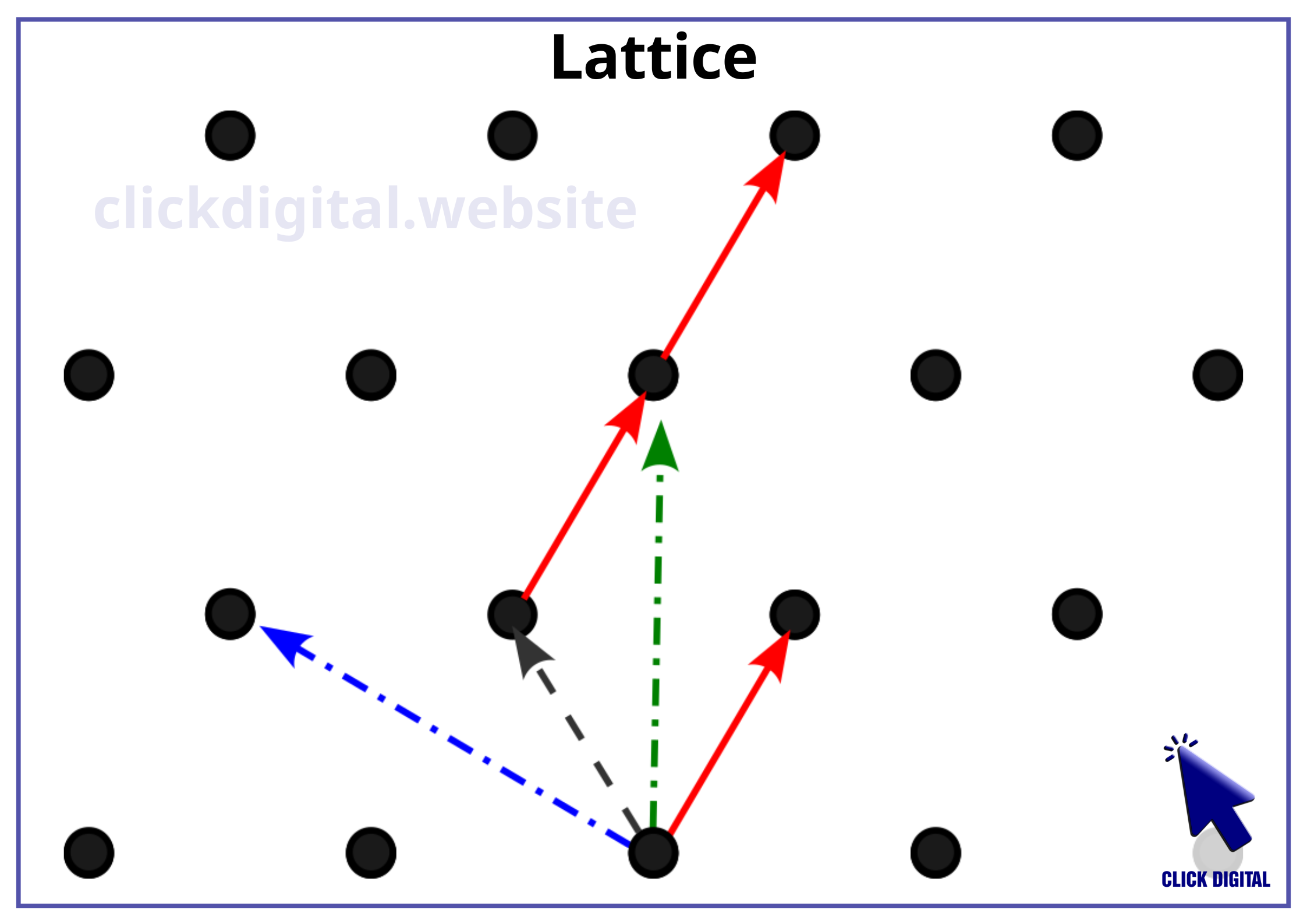
Mạng lưới (lattice) trong mật mã học được hiểu là một tập hợp các điểm trong không gian n chiều được tạo thành bằng cách kết hợp tuyến tính các vector cơ sở. Nói cách khác, mạng lưới là một tập hợp các điểm có dạng:

v = a₁b₁ + a₂b₂ + ... + anbn

trong đó a₁, a₂, …, an là các số nguyên và b₁, b₂, …, bn là các vector cơ sở của mạng lưới.

Ví dụ:

Hãy tưởng tượng bạn có hai vector cơ sở trong không gian 2 chiều:

• b₁ = (1, 0)
• b₂ = (0, 1)

Bằng cách kết hợp tuyến tính hai vector cơ sở này với các số nguyên, bạn có thể tạo ra một mạng lưới gồm các điểm như sau:

• (0, 0): 0 * b₁ + 0 * b₂
• (1, 0): 1 * b₁ + 0 * b₂
• (0, 1): 0 * b₁ + 1 * b₂
• (1, 1): 1 * b₁ + 1 * b₂
• (2, 0): 2 * b₁ + 0 * b₂
• (0, 2): 0 * b₁ + 2 * b₂
• …v.v.

Các điểm này sẽ tạo thành một mạng lưới các điểm cách đều nhau và song song trên mặt phẳng 2 chiều.

Ý nghĩa của mạng lưới trong Cryptography:

Mạng lưới được sử dụng trong Cryptography bởi vì chúng có một số tính chất thú vị:

• Cấu trúc đều đặn: Các điểm trong mạng lưới được sắp xếp đều đặn và có cấu trúc nhất định. Tính chất này có thể được sử dụng để thiết kế các thuật toán mật mã hiệu quả.
• Tính toán dễ dàng: Các phép toán trên mạng lưới, chẳng hạn như cộng và trừ, rất dễ thực hiện. Điều này giúp cho các thuật toán mật mã dựa trên mạng lưới hoạt động nhanh hơn.
• Liên hệ với các vấn đề mật mã: Một số vấn đề mật mã có thể được chuyển đổi thành các vấn đề liên quan đến mạng lưới. Ví dụ, vấn đề số ẩn (HNP – Hidden Number Problem) có thể được giải quyết bằng cách sử dụng giải thuật thu nhỏ cơ sở mạng lưới.

2. Cần có kiến thức gì để hiểu về Lattice trong Cryptography?

Định nghĩa về lattice có thể hơi khó hiểu nếu bạn chưa có kiến thức nền tảng về toán học, đặc biệt là đại số tuyến tính. Để hiểu rõ hơn về lattice, bạn cần nắm vững các kiến thức sau:

1. Vector và không gian vector:

• Vector: Là một đại lượng có độ lớn và hướng. Vector được biểu diễn bằng một mũi tên.
• Không gian vector: Là một tập hợp các vector mà có thể thực hiện phép cộng vector và phép nhân vô hướng.

2. Kết hợp tuyến tính:

• Kết hợp tuyến tính của các vector là việc cộng các vector với nhau, mỗi vector được nhân với một hệ số vô hướng (số thực hoặc số phức).

3. Tập hợp các điểm:

• Lattice là một tập hợp các điểm đặc biệt trong không gian vector, được tạo ra bằng cách kết hợp tuyến tính các vector cơ sở với các hệ số vô hướng là các số nguyên.

4. Cơ sở mạng lưới:

• Cơ sở mạng lưới là một tập hợp các vector tuyến tính độc lập, có thể tạo ra tất cả các điểm trong mạng lưới.

Để dễ hình dung, bạn có thể tưởng tượng:

• Mạng lưới 1 chiều: Là một tập hợp các điểm nằm trên một đường thẳng, cách đều nhau. Vector cơ sở của mạng lưới này chỉ là một vector có hướng trùng với đường thẳng.
• Mạng lưới 2 chiều: Là một tập hợp các điểm nằm trên một mặt phẳng, cách đều nhau theo các hướng song song. Mạng lưới này có hai vector cơ sở, tạo thành một hình bình hành.

Ví dụ:

• Mạng lưới trong hình 2 chiều với hai vector cơ sở b1 = (1, 0) và b2 = (0, 1) là tập hợp các điểm có dạng v = (a, b) với a, b là các số nguyên. Các điểm này tạo thành một mạng lưới hình vuông đều.

3. Giải thuật thu nhỏ cơ sở mạng lưới (Lattice Basis Reduction)

Giải thuật thu nhỏ cơ sở mạng lưới (lattice basis reduction) là một loại giải thuật tìm ra một cơ sở mới của mạng lưới, trong đó các vector cơ sở có độ dài ngắn hơn và gần với trực giao hơn. Hai giải thuật phổ biến nhất là LLL (Lenstra–Lenstra–Lovász) và BKZ (Block Korkine–Zolotarev).

Ý nghĩa của giải thuật thu nhỏ cơ sở mạng lưới trong Cryptography:

Giải thuật thu nhỏ cơ sở mạng lưới đóng vai trò quan trọng trong tấn công Lattice. Bởi vì các cuộc tấn công Lattice thường dựa trên việc tìm ra các vector ngắn nhất trong mạng lưới. Việc thu nhỏ cơ sở mạng lưới giúp giảm thiểu độ dài của các vector cơ sở, khiến cho việc tìm ra các vector ngắn nhất trở nên dễ dàng hơn.

Các loại tấn công Lattice trong Cryptography

Có nhiều loại tấn công Lattice trong Cryptography, nhưng hai loại phổ biến nhất là:

1. Tấn công dựa trên vấn đề số ẩn: Vấn đề số ẩn (HNP – Hidden Number Problem) là vấn đề tìm ra một số ẩn α trong một trường hữu hạn Fp, biết các cặp (ti
, MSB,p(αti)). Các cặp này là khóa công khai. Các cuộc tấn công HNP thường được sử dụng để khai thác các lỗ hổng trong việc tạo chữ ký số, nơi một số bit của nonce (số ngẫu nhiên) được sử dụng trong quá trình tạo chữ ký được tiết lộ.

2. Tấn công dựa trên phương trình đa thức: Phương pháp này dựa trên giải thuật thu nhỏ cơ sở mạng lưới để tìm ra các nghiệm nhỏ của phương trình đa thức mod N, trong đó N là khóa công khai. Loại tấn công này có thể được sử dụng để tấn công các hệ thống mã hóa dựa trên đa thức, như RSA.

Tấn công Lattice trong Cryptography để làm gì?

Tấn công Lattice được sử dụng để tấn công các thuật toán ký số như DSA và ECDSA, cũng như các hệ thống mã hóa như RSA. Các cuộc tấn công này thường dựa trên giả định rằng kẻ tấn công có thể truy cập một số bit của nonce.

Ví dụ:

• DSA: Trong DSA, nonce là một số ngẫu nhiên được sử dụng để tạo chữ ký. Nếu kẻ tấn công có thể lấy được một số bit của nonce, chúng có thể sử dụng tấn công Lattice để tìm ra khóa bí mật của DSA.
• RSA: Tấn công Lattice có thể được sử dụng để tấn công RSA bằng cách khai thác các lỗ hổng trong việc tạo khóa RSA hoặc trong việc sử dụng khóa RSA để giải mã thông tin. Ví dụ, nếu kẻ tấn công biết một phần của khóa bí mật RSA, chúng có thể sử dụng tấn công Lattice để tìm ra toàn bộ khóa bí mật.

Lợi thế và nhược điểm của tấn công Lattice

Lợi thế	Nhược điểm
Hiệu quả: Tấn công Lattice có thể hiệu quả trong việc tìm ra khóa bí mật, đặc biệt khi kích thước khóa bí mật nhỏ. Giải thuật thu nhỏ cơ sở mạng lưới có thể tìm ra các vector ngắn nhất trong mạng lưới với độ chính xác cao, đặc biệt khi kích thước mạng lưới không quá lớn. Điều này giúp tấn công nhanh chóng và hiệu quả hơn so với các phương pháp tấn công khác.	Phức tạp: Các giải thuật tấn công Lattice thường phức tạp và khó triển khai. Các giải thuật thu nhỏ cơ sở mạng lưới, như LLL hay BKZ, có thể phức tạp và yêu cầu nhiều tài nguyên tính toán. Việc thiết kế và triển khai các cuộc tấn công Lattice đòi hỏi kiến thức chuyên sâu về toán học, thuật toán và mật mã.
Khả năng ứng dụng rộng rãi: Nó có thể được áp dụng cho nhiều thuật toán ký số và hệ thống mã hóa khác nhau. Tấn công Lattice có thể được ứng dụng cho nhiều thuật toán mật mã khác nhau, bao gồm cả các thuật toán được sử dụng rộng rãi như RSA, DSA, ECDSA. Điều này làm cho tấn công Lattice trở thành một mối đe dọa tiềm ẩn đối với nhiều hệ thống mật mã.	Giả định: Chúng dựa trên giả định rằng kẻ tấn công có thể truy cập một số bit của nonce. Giả định này có thể là một hạn chế lớn, bởi vì trong thực tế, kẻ tấn công thường không dễ dàng có được thông tin về nonce. Việc tiếp cận thông tin về nonce thường yêu cầu thực hiện các cuộc tấn công kênh phụ (side-channel attacks) phức tạp, dễ bị phát hiện và có thể không mang lại kết quả mong muốn.

Giải thích về nhược điểm Giả định:

Nhược điểm giả định trong tấn công Lattice là vì phương pháp này thường dựa trên giả định rằng kẻ tấn công có thể truy cập một số bit của nonce. Tuy nhiên, trong thực tế, việc lấy được thông tin về nonce không phải lúc nào cũng dễ dàng.

Nonce là một số ngẫu nhiên được sử dụng trong các thuật toán mật mã để đảm bảo tính độc lập của mỗi chữ ký. Kẻ tấn công cần có khả năng thu thập thông tin về nonce từ các kênh bên (side channel), chẳng hạn như:

• Phân tích thời gian: Kẻ tấn công đo thời gian thực hiện các thao tác trong quá trình tạo chữ ký để tìm ra các điểm khác biệt nhỏ có thể tiết lộ thông tin về nonce.
• Phân tích năng lượng: Kẻ tấn công phân tích lượng năng lượng tiêu thụ trong khi thiết bị tạo chữ ký đang hoạt động để tìm ra các mẫu tiết lộ thông tin về nonce.
• Phân tích lỗi: Kẻ tấn công cố gắng gây lỗi cho thiết bị tạo chữ ký và quan sát các phản hồi của thiết bị để tìm ra thông tin về nonce.

Nếu không có thông tin về nonce, tấn công Lattice sẽ khó thực hiện hoặc thậm chí là không thể. Vì vậy, giả định rằng kẻ tấn công có thể truy cập một số bit của nonce là một nhược điểm lớn của tấn công Lattice.

Ví dụ, nếu nonce là một số hoàn toàn ngẫu nhiên và không bị tiết lộ thông tin qua các kênh bên, thì kẻ tấn công sẽ không thể sử dụng tấn công Lattice để tìm ra khóa bí mật.

Các ví dụ thực tế về tấn công Lattice trong Cryptography

Tấn công Lattice là một phương pháp tấn công hiệu quả, đặc biệt khi tấn công các hệ thống mật mã có khóa bí mật nhỏ. Nó dựa trên lý thuyết mạng lưới và giải thuật thu nhỏ cơ sở mạng lưới. Click Digital sẽ giới thiệu thêm một số ví dụ thực tế về các cuộc tấn công Lattice thành công trong quá khứ để minh họa cho sức mạnh của phương pháp này.

1. Tấn công của Nguyen vào GPG

Năm 2003, Nguyen đã phát hiện ra một lỗ hổng trong phần mềm mã hóa email mã nguồn mở GPG (GNU Privacy Guard) phiên bản 1.2.3. Lỗ hổng này liên quan đến việc GPG sử dụng thuật toán ký số ElGamal, nơi khóa bí mật của người ký được tạo ra bằng cách chọn một số ngẫu nhiên có độ dài bằng 3/2 độ dài của qbit (một giá trị được xác định dựa trên độ dài của khóa công khai p).

Cách tấn công: Nguyen đã chứng minh rằng nếu kẻ tấn công biết được một chữ ký hợp lệ (a, b) của GPG, chúng có thể tìm ra khóa bí mật x dựa trên công thức: ax + bk = m (mod p-1), trong đó a, b, k và m là các giá trị đã biết. Bằng cách sử dụng các giải thuật thu nhỏ cơ sở mạng lưới, Nguyen đã tìm ra được một vector ngắn nhất trong mạng lưới, nhờ đó tìm ra được khóa bí mật x.

Cuộc tấn công của Nguyen đã chứng minh rằng GPG dễ bị tổn thương trước các cuộc tấn công Lattice, bởi vì nó sử dụng các khóa bí mật quá ngắn. Sau đó, GPG đã loại bỏ ElGamal và áp dụng các thuật toán ký số an toàn hơn.

2. Tấn công RSA với khóa bí mật nhỏ của Boneh & Durfee

Năm 1996, Boneh & Durfee đã phát triển một cuộc tấn công vào hệ thống mã hóa RSA với khóa bí mật nhỏ. Cuộc tấn công này dựa trên “vấn đề số ẩn” (HNP), và sử dụng phương pháp thu nhỏ cơ sở mạng lưới để tìm ra khóa bí mật.

Cách tấn công: Boneh & Durfee đã chứng minh rằng nếu kẻ tấn công biết được một số bit của khóa bí mật d, chúng có thể sử dụng một giải thuật thu nhỏ cơ sở mạng lưới để tìm ra khóa bí mật đầy đủ. Họ đã sử dụng phương pháp “small inverse problem” để tìm ra một số ẩn α, từ đó tìm ra được khóa bí mật d.

Cuộc tấn công này đã chứng minh rằng RSA với khóa bí mật nhỏ có thể dễ dàng bị tấn công. Nó đã thúc đẩy sự phát triển của các thuật toán mã hóa RSA mới với khóa bí mật lớn hơn, nhằm tăng cường độ an toàn.

3. Tấn công vào ESIGN và NBD

ESIGN và NBD là hai thuật toán ký số được sử dụng trong mật mã học. Tuy nhiên, cả hai thuật toán này đều dễ bị tổn thương trước các cuộc tấn công Lattice. Các cuộc tấn công này dựa trên việc kẻ tấn công có thể tiếp cận một số bit của nonce được sử dụng trong quá trình tạo chữ ký.

• Tấn công ESIGN: Proos (2003) đã chứng minh rằng ESIGN dễ bị tổn thương trước các cuộc tấn công Lattice, nếu kẻ tấn công biết được một số bit của nonce. Cuộc tấn công này dựa trên việc chuyển đổi vấn đề tìm kiếm khóa bí mật thành vấn đề “tìm kiếm ước chung gần đúng”.
• Tấn công NBD: Proos (2003) đã chỉ ra rằng thuật toán ký số NBD cũng dễ bị tấn công bởi Lattice, nếu kẻ tấn công biết được một số bit của nonce.

Suy ra: Các cuộc tấn công Lattice đã chứng minh rằng nhiều thuật toán mật mã hiện nay dễ bị tổn thương trước các cuộc tấn công này. Điều này đã thúc đẩy sự phát triển của các thuật toán mật mã tốt hơn và an toàn hơn. Tuy nhiên, các cuộc tấn công Lattice vẫn là một mối đe dọa tiềm ẩn đối với mật mã học, và các nhà nghiên cứu đang tiếp tục nghiên cứu và tìm cách phòng chống chúng.

Nhận xét về tấn công Lattice

Có thể thấy rằng tấn công Lattice là một mối đe dọa nghiêm trọng đối với các hệ thống mật mã hiện nay. Tuy nhiên, chúng không phải là không thể phòng chống. Các nhà phát triển mật mã đang nỗ lực để tăng cường bảo mật của các thuật toán ký số và hệ thống mã hóa trước các cuộc tấn công này.

Kết luận

Tấn công Lattice là một phương pháp tấn công hiệu quả, đặc biệt khi tấn công các hệ thống mật mã có khóa bí mật nhỏ. Tuy nhiên, chúng có thể rất phức tạp để triển khai và phụ thuộc vào giả định rằng kẻ tấn công có thể truy cập một số bit của nonce. Mặc dù là mối đe dọa, các cuộc tấn công Lattice đã thúc đẩy sự phát triển của các kỹ thuật mật mã tốt hơn và an toàn hơn.

Click Digital hy vọng bài viết này đã giúp mọi người hiểu rõ hơn về tấn công Lattice trong Cryptography.